Gambler's Fallacy
Your progress on this bias test won't be saved after you close your browser.
Understanding Gambler's Fallacy
Gambler's Fallacy
The mistaken belief that past random events affect the likelihood of future outcomes in independent situations.
Overview
Gambler's fallacy is the erroneous belief that if an event occurs more frequently than expected in the past, it will occur less frequently in the future (or vice versa). This cognitive bias leads people to misunderstand random sequences and make poor judgments about probability in scenarios ranging from gambling to financial investing to everyday decision-making.
Key Points:
- Each independent event maintains the same probability regardless of previous outcomes
- People falsely attribute meaning to randomness and see patterns where none exist
- This bias can lead to costly mistakes in risk assessment and resource allocation
- Also known as the "Monte Carlo fallacy" after a famous 1913 casino incident
Impact: The gambler's fallacy distorts decision-making across numerous domains. Investors might sell stocks after a series of gains, expecting a downturn, while project managers might underestimate risks after several successful initiatives. In each case, the failure to recognize statistical independence leads to suboptimal choices.
Practical Importance: Understanding this bias is crucial for anyone making decisions under uncertainty. By recognizing when events are truly independent, you can avoid the trap of expecting "balancing" outcomes and instead make choices based on actual probabilities rather than perceived patterns.
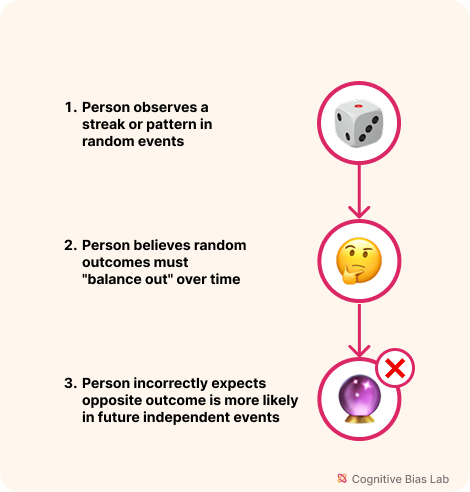
Visual representation of Gambler's Fallacy (click to enlarge)
Examples of Gambler's Fallacy
Here are some real-world examples that demonstrate how this bias affects our thinking:
Psychological Study Simulation
The Gambler's Fallacy
Discover why people believe that after several heads, a coin is 'due' for tails - even though each flip remains an independent 50/50 chance.
Roulette Table Misjudgment
At a casino in Monaco, after the roulette ball landed on black 26 times in a row, players began placing increasingly large bets on red, believing it was "due" to appear. They lost millions as the streak extended to black appearing 15 more times. This illustrates how the gambler's fallacy causes people to misinterpret randomness and make decisions based on the false belief that independent events somehow balance out.
Investment Strategy Error
After observing that a particular industry has experienced five consecutive quarters of growth, a financial analyst advises clients that a downturn is "inevitable" and recommends selling those assets. This decision isn't based on fundamental analysis or changing market conditions, but solely on the mistaken belief that the streak must end. When the industry continues to perform well, clients miss substantial gains due to this probabilistic reasoning error.
How to Overcome Gambler's Fallacy
Here are strategies to help you recognize and overcome this bias:
Think in Probabilities
Ask if past outcomes truly affect future ones. If not, treat each event as independent with unchanged odds.
Log Your Reasoning
Write down your decision logic. Watch for signs like 'it's due'—a clue you're misjudging randomness.
Test Your Understanding
Challenge yourself with these questions to see how well you understand this cognitive bias:
A cryptocurrency has shown positive returns for 7 consecutive days. Your colleague argues that it's time to sell because "it's bound to drop soon." What cognitive error is influencing this reasoning?
Academic References
- Tversky, A., & Kahneman, D. (1971). Belief in the law of small numbers. Psychological Bulletin, 76(2), 105–110.
- Wang, D., & Li, Y. (2025). The number of available sample observations modulates gambler’s fallacy in betting behaviors. Scientific Reports, 15(1).
- Krébesz, R., Ötvös, D. K., & Fekete, Z. (2023). Non-problem gamblers show the same cognitive distortions while playing slot machines as problem gamblers, with no loss of control and reduced reality control, though – An experimental study on gambling. Frontiers in Psychology, 14.