Base Rate Fallacy
Your progress on this bias test won't be saved after you close your browser.
Understanding Base Rate Fallacy
Base Rate Fallacy
We're naturally drawn to specific, vivid details while ignoring broader statistical realities. This mental blindspot leads us to overestimate unlikely events and make poor probability judgments in everything from medical decisions to risk assessment.
Overview
Base rate fallacy occurs when we focus too heavily on new, specific information while neglecting relevant background statistics (base rates). This cognitive error leads us to make probability misjudgments by overweighting vivid details and underweighting the underlying statistical context.
Key Points:
- Base rates provide the fundamental statistical backdrop against which new information should be interpreted.
- Our minds are naturally drawn to specific, concrete details over abstract statistical information.
- This bias affects critical decisions in medicine, law, finance, and everyday risk assessment.
Impact: Ignoring base rates can lead to serious misjudgments. For instance, if a medical test for a rare disease (affecting only 1 in 10,000 people) has a 99% accuracy rate, a positive result still likely represents a false positive—but doctors and patients often overlook this statistical reality, potentially leading to unnecessary treatments.
Practical Importance: Recognizing this bias helps us make more rational judgments by properly weighing new information against established background probabilities, especially in high-stakes situations involving risk assessment, resource allocation, or diagnosis.
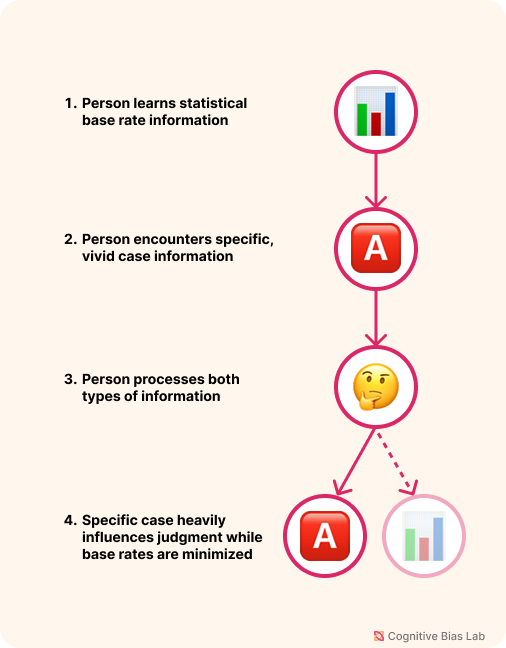
Visual representation of Base Rate Fallacy (click to enlarge)
Examples of Base Rate Fallacy
Here are some real-world examples that demonstrate how this bias affects our thinking:
Psychological Study Simulation
Base Rate Fallacy Simulation
Experience how we tend to ignore general statistical information (base rates) and focus too much on specific details, leading to incorrect probability judgments.
Medical Diagnosis Dilemma
A doctor tells a patient their test for a rare disease came back positive, and the test is 95% accurate. The patient panics, assuming they likely have the disease. However, since the disease occurs in only 1 in 1,000 people (the base rate), even with a positive result, the actual probability of having the disease is still quite low. The patient and doctor both overlook the critical base rate information, leading to unnecessary anxiety and potentially harmful treatments.
Security Screening Paradox
An airport implements a facial recognition system that is 99.9% accurate at identifying persons of interest. When it flags someone, security personnel typically conduct intensive screening, assuming the person is highly likely to be a threat. However, with actual threats being extremely rare (perhaps 1 in 10 million travelers), most flagged individuals are false positives. By neglecting this base rate, resources are wasted and innocent travelers face unnecessary inconvenience.
How to Overcome Base Rate Fallacy
Here are strategies to help you recognize and overcome this bias:
Start thinking in base rates
Always ask for the original probability before new data. Use Bayes' rule to update your estimate logically.
Use Natural Frequencies
Convert percentages into real-world counts e.g., '10 out of 1,000'—to make true probabilities easier to grasp.
Test Your Understanding
Challenge yourself with these questions to see how well you understand this cognitive bias:
A company uses a hiring algorithm that correctly identifies top performers 90% of the time. If only 5% of applicants would truly be top performers, what error are they making if they hire everyone the algorithm recommends?
Academic References
- Kahneman, D., & Tversky, A. (1973). On the psychology of prediction. Psychological Review, 80(4), 237-251.
- Dethier, C. (2025). Who’s Afraid of the Base-Rate Fallacy? Philosophy of Science, 92(2), 453–469.
- Pennycook, G., Trippas, D., Handley, S. J., & Thompson, V. A. (2013). Base rates: Both neglected and intuitive. Journal of Experimental Psychology Learning Memory and Cognition, 40(2), 544–554.